Đề bài
Gọi M là một điểm nằm trên đường tròn (O). Vẽ đường tròn (O’) đường kính OM. Bán kính OA của (O) cắt (O’) tại B. Chứng minh rằng hai cung MA và MB bằng nhau.
Phương pháp giải - Xem chi tiết
Sử dụng: Xét (O):\(\widehat {AOB} = \alpha \Rightarrow {l_{\overparen{AB}}} =\dfrac {{\pi R\alpha } }{{180}}\)
Lời giải chi tiết
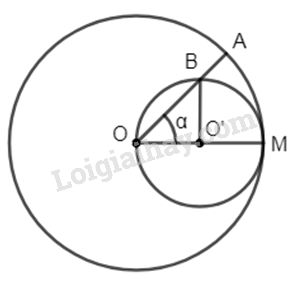
Đặt \(\widehat {MOA} = \alpha \)
\( \Rightarrow \widehat {MO'B} = 2\alpha \) ( góc ngoài của \(∆OO’B\))
Gọi \(l_1\) là độ dài cung MA của đường tròn (O), \({l_1} = \dfrac{{\pi .OM.\alpha } }{ {180}}\)
Độ dài cung MB của đường tròn (O’) bán kính \(\dfrac{{OM} }{ 2}\) :
Có \({l_2} = \dfrac{{\pi {{OM} \over 2}.2\alpha } }{ {180}} =\dfrac {{\pi OM\alpha } }{ {180}}\).
Vậy \({l_1} = {l_2}\) (đpcm).
soanvan.me
