Phép cộng các số tự nhiên có tính chất nào dưới đây?
A. Tính chất giao hoán
B. Tính chất kết hợp
C. Tính chất cộng với số \(0\)
D. Tất cả các đáp án trên đều đúng
D. Tất cả các đáp án trên đều đúng
Xem lại lí thuyết về các tính chất của phép cộng các số tự nhiên.
Phép cộng các số tự nhiên có tính chất:
- Tính chất giao hoán: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi.
- Tính chất kết hợp: Khi cộng một tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba.
- Tính chất cộng với số \(0\): Mọi số tự nhiên cộng với số \(0\) đều bằng chính số đó.
Vậy các đáp án A, B, C đều đúng.
Biểu thức \(a + b \times 2 - c\) được gọi là:
A. Biểu thức có chứa một chữ
B. Biểu thức có chứa hai chữ
C. Biểu thức có chứa ba chữ
C. Biểu thức có chứa ba chữ
Xem lại lí thuyết về các biểu thức có chứa chữ.
Biểu thức \(a + b \times 2 - c\) bao gồm các số, dấu tính và ba chữ \(a,\,\,b,\,\,c\).
Vậy biểu thức đã cho là biểu thức có chứa ba chữ.
Điền số thích hợp vào ô trống:
\(28745+63149=\)
\(28745+63149=\)
Muốn cộng hai số tự nhiên ta có thể làm như sau:
- Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
- Cộng các chữ số ở từng hàng theo thứ tự từ phải sang trái, tức là từ hàng đơn vị đến hàng chục, hàng trăm, hàng nghìn, … .
Ta đặt tính và thực hiện tính như sau:
\(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{28745}\\{63149}\end{array}}\\\hline{\,\,\,\,91894}\end{array}\)
Vậy \(28745 + 63149 = \,91894\).
Đáp án đúng điền vào ô trống là \(91894\).
Với \(a = 6,\,b = 113\) thì giá trị của biểu thức \(1357 - 38 \times a + b\) là:
A. \(1016\)
B. \(1242\)
C. \(7914\)
D. \(8027\)
B. \(1242\)
Thay \(a = 6,\,b = 113\) vào biểu thức \(1357 - 38 \times a + b\) rồi tính giá trị biểu thức đó.
Nếu \(a = 6,\,b = 113\) thì:
\(1357 - 38 \times a + b = 1357 - 38 \times 6 + 113\)
\(= 1357 - 228 + 113\)
\(= 1129 + 113 \)
\(= 1242\)
Vậy với \(a = 6,\,b = 113\) thì biểu thức \(1357 - 38 \times a + b\) có giá trị là \(1242\).
Điền số thích hợp vào ô trống:
_Cau5.jpg)
Trong hình trên có
góc vuông,
góc nhọn,
góc tù,
góc bẹt.
Trong hình trên có
góc vuông,
góc nhọn,
góc tù,
góc bẹt.
Quan sát hình vẽ để xác định các góc.
Áp dụng các tính chất về các góc: góc nhọn bé hơn góc vuông; góc tù lớn hơn góc vuông; góc bẹt bằng hai góc vuông.
Hình đã cho có:
- \(4\) góc vuông:
+ Góc vuông đỉnh M; cạnh MA, MN.
+ Góc vuông đỉnh M; cạnh MN, MB.
+ Góc vuông đỉnh N; cạnh ND, NM.
+ Góc vuông đỉnh N; cạnh NM, NC
- \(6\) góc nhọn:
+ Góc nhọn đỉnh B; cạnh BA, BC.
+ Góc nhọn đỉnh B; cạnh BA, BN.
+ Góc nhọn đỉnh B; cạnh BN, BC.
+ Góc nhọn đỉnh D; cạnh DA, DC.
+ Góc nhọn đỉnh N; cạnh NM, NB.
+ Góc nhọn đỉnh N; cạnh NB, NC.
- \(3\) góc tù:
+ Góc tù đỉnh A; cạnh AB, AD.
+ Góc tù đỉnh C; cạnh CB, CD.
+ Góc tù đỉnh N; cạnh NB, ND.
- \(2\) góc bẹt:
+ Góc bẹt đỉnh M; cạnh MA, MB.
+ Góc bẹt đỉnh N; cạnh NC, ND.
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là \(4, 6, 3, 2\).
Điền số thích hợp vào ô trống để tính bằng cách thuận tiện:
\(5147 + 6954 + 2853 + 3046\)
\(=(5147+\)
\()+(\)
\(+3046)\)
\(=\)
\(+\)
\(=\)
\(5147 + 6954 + 2853 + 3046\)
\(=(5147+\)
\()+(\)
\(+3046)\)
\(=\)
\(+\)
\(=\)
Áp dụng tính chất kết hợp của phép cộng để nhóm các số có tổng là số tròn nghìn.
Ta có:
$\begin{array}{l}5147 + 6954 + 2853 + 3046 = \left( {5147 + 2853} \right) + \left( {6954 + 3046} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 8000 + 10000\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 18000\end{array}$
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trên xuống dưới, từ trái sang phải là \(2853\,\,;\,\,6954\,;\,\,8000\,\,;\,\,10000\,\,;\,\,18000\).
Tìm \(y\) biết: \(43082 - 5 \times y = 3489 + 4398\).
A. \(y = 7033\)
B. \(y = 7035\)
C. \(y = 7037\)
D. \(y = 7039\)
D. \(y = 7039\)
- Tính giá trị vế phải.
- Tìm \(5 \times y;\,5 \times y\) ở vị trí số trừ, muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
- Tìm \(y;\,y\) ở vị trí thừa số, muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
\(\begin{array}{l}43082 - 5 \times y = 3489 + 4398\\43082 - 5 \times y = 7887\\5 \times y = 43082 - 7887\\5 \times y = 35195\\y = 35195:5\\y = 7039\end{array}\)
Tổng của hai số là $5648$. Nếu thêm vào số lớn $532$ đơn vị và bớt ở số bé đi \(235\) đơn vị thì được tổng mới là:
A. \(6415\)
B. \(5945\)
C. \(5351\)
D. \(4881\)
B. \(5945\)
Nếu thêm vào một số hạng bao nhiêu đơn vị thì tổng tăng thêm bấy nhiêu đơn vị; ngược lại, nếu bớt ở một số hạng bao nhiêu đơn vị thì tổng giảm đi bấy nhiêu đơn vị.
Nếu thêm vào số lớn $532$ đơn vị và bớt ở số bé đi \(235\) đơn vị thì được tổng mới là:
$5648 + 532 - 235 = 5945$
Một tổ nông dân thu hoạch thóc ở một nông trường. Ngày thứ nhất thu hoạch được $6870kg$ thóc, ngày thứ hai thu hoạch số thóc bằng một nửa số thóc ngày thứ nhất, ngày thứ ba thu hoạch gấp \(3\) lần ngày thứ hai. Hỏi cả \(3\) ngày tổ nông dân thu hoạch được bao nhiêu ki-lô-gam thóc?
A. $10305kg$
B. $13735kg$
C. $20610kg$
D. $61830kg$
C. $20610kg$
- Tính số thóc thu hoạch ngày thứ hai ta lấy số thóc thu hoạch ngày thứ nhất chia cho \(2\).
- Tính số thóc thu hoạch ngày thứ ba ta lấy số thóc thu hoạch ngày thứ hai nhân với \(3\).
- Tính tổng số thóc thu trong ba ngày = số thóc ngày thứ nhất + số thóc ngày thứ hai + số thóc ngày thứ ba.
Ngày thứ hai tổ nông dân thu hoạch được số ki-lô-gam thóc là:
$6870:2 = 3435\left( {kg} \right)$
Ngày thứ ba tổ nông dân thu hoạch được số ki-lô-gam thóc là:
$3435 \times 3 = 10305\left( {kg} \right)$
Cả \(3\) ngày tổ nông dân thu hoạch được số ki-lô-gam thóc là:
$6870 + 3435 + 10305 = 20610\left( {kg} \right)$
Đáp số: $20610kg$ thóc.
Điền số thích hợp vào ô trống:
Cho hai số có tổng là số bé nhất có 4 chữ số và hiệu là số chẵn lớn nhất có 2 chữ số.
Vậy số lớn là
, số bé là
Cho hai số có tổng là số bé nhất có 4 chữ số và hiệu là số chẵn lớn nhất có 2 chữ số.
Vậy số lớn là
, số bé là
- Tìm tổng và hiệu của hai số: số bé nhất có 4 chữ số là $1000$, số chẵn lớn nhất có \(2\) chữ số là $98$.
- Áp dụng công thức tìm hai số khi biết tổng và hiệu của hai số đó:
Số bé = (tổng – hiệu) : $2$ ; Số lớn = (tổng + hiệu) : $2$
Số bé nhất có 4 chữ số là $1000$. Do đó tổng của \(2\) số đó là $1000$.
Số chẵn lớn nhất có \(2\) chữ số là $98$. Do đó hiệu của \(2\) số đó là $98$.
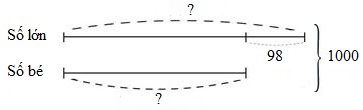
Số bé là:
$(1000 - 98):2 = 451$
Số lớn là:
$1000 - 451 = 549$
Đáp số: Số lớn: \(549\); số bé: \(451\).
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là \(549\,\,;\,\,451\).
Điền số thích hợp vào ô trống:
Trong năm học vừa qua, khối \(3\), khối \(4\) và khối \(5\) của trường tiểu học Kim Đồng góp được $1250$ quyển vở tặng các bạn vùng lũ lụt. Biết khối \(3\) góp được \(377\) quyển, khối \(4\) góp được nhiều hơn khối \(5\) là \(45\) quyển.
Vậy khối \(4\) góp được
quyển vở.
Khối \(5\) góp được
quyển vở.
Trong năm học vừa qua, khối \(3\), khối \(4\) và khối \(5\) của trường tiểu học Kim Đồng góp được $1250$ quyển vở tặng các bạn vùng lũ lụt. Biết khối \(3\) góp được \(377\) quyển, khối \(4\) góp được nhiều hơn khối \(5\) là \(45\) quyển.
Vậy khối \(4\) góp được
quyển vở.
Khối \(5\) góp được
quyển vở.
- Tìm số vở khối \(4\) và khối \(5\) cùng góp được ta lấy tổng số vở trừ đi số vở khối \(3\) đã góp.
- Tìm số vở khối \(4\) góp và số vở khối \(5\) góp theo công thức tìm hai số khi biết tổng và hiệu của hai số đó:
Số bé = (tổng – hiệu) : $2$ ; Số lớn = (tổng + hiệu) : $2$
Khối \(4\) và khối \(5\) góp được số quyển vở là:
$1250 - 377 = 873$ (quyển)
Khối \(4\) góp được số quyển vở là:
$(873 + 45):2 = 459$ (quyển)
Khối \(5\) góp được số quyển vở là:
$873 - 459 = 414$ (quyển)
Đáp số: Khối \(4\,:\,459\) quyển vở;
Khối \(5\,:\,414\) quyển vở.
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(459\,;\,\,414\).
Một mảnh đất hình chữ nhật có chu vi là \(86m\). Biết nếu chiều rộng tăng thêm \(8m\), chiều dài giảm đi $17m$ thì mảnh đất đó có dạng hình vuông. Diện tích mảnh đất đó là:
A. \(306{m^2}\)
B. \(316{m^2}\)
C. \(326{m^2}\)
D. \(336{m^2}\)
A. \(306{m^2}\)
- Tìm số đo nửa chu vi mảnh đất hình chữ nhật.
- Tìm hiệu số đo chiều dài và chiều rộng.
- Tìm chiều dài và chiều rộng dựa vào công thức tìm hai số khi biết tổng và hiệu của hai số :
Số bé = (tổng – hiệu) : $2$ ; Số lớn = (tổng + hiệu) : $2$
- Tính diện tích = chiều dài × chiều rộng.
Nửa chu vi hình chữ nhật là:
$86:2 = 43(m)$
Vì nếu chiều rộng tăng thêm \(8m\), chiều dài giảm đi $17m$ thì mảnh đất đó có dạng hình vuông nên hiệu giữa số đo chiều dài và chiều rộng là:
\(8m + 17m = 25(m)\)
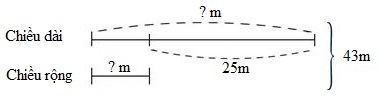
Chiều rộng của mảnh đất hình chữ nhật đó là:
\((43 - 25):2 = 9\,\,(m)\)
Chiều dài của của mảnh đất hình chữ nhật đó là:
\(9 + 25 = 34\,\,(m)\)
Diện tích của của mảnh đất hình chữ nhật đó là:
\(34\,\, \times 9 = 306\,\,({m^2})\)
Đáp số: \(306{m^2}\)
Điền số thích hợp vào ô trống:
Người ta đếm được trên sân có \(262\) cái chân gà và chân chó. Biết số chân gà nhiều hơn số chân chó là $38$ cái.
Vậy trên sân có
con gà và
con chó.
Người ta đếm được trên sân có \(262\) cái chân gà và chân chó. Biết số chân gà nhiều hơn số chân chó là $38$ cái.
Vậy trên sân có
con gà và
con chó.
- Tìm số chân chó và số chân gà dựa vào công thức tìm hai số khi biết tổng và hiệu của hai số :
Số bé = (tổng – hiệu) : $2$ ; Số lớn = (tổng + hiệu) : $2$
- Mỗi con chó có \(4\) chân nên tìm số con chó ta lấy số chân chó chia cho \(4\).
- Mỗi con gà có \(2\) chân nên tìm số con gà ta lấy số chân gà chia cho \(2\).
Số chân gà là:
\((262 + 38):2 = 150\) (cái chân)
Số chân chó là:
\(262 - 150 = 112\) (cái chân)
Trên sân có số con gà là:
$150:2 = 75$ (con)
Trên sân có số con chó là:
$112:4 = 28$ (con)
Đáp số: Số con gà: \(75\) con;
Số con chó: \(28\) con.
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là \(75\,\,;\,\,28\).
Hai người thợ dệt được \(258m\) vải. Nếu thợ thứ nhất dệt thêm \(36m\) vải và thợ thứ hai dệt bớt đi \(15m\) vải thì thợ thứ nhất sẽ dệt nhiều hơn thợ thứ hai là \(27m\) vải. Hỏi mỗi người thợ dệt được bao nhiêu mét vải?
A. Thợ thứ nhất: \(125m\); thợ thứ hai: \(133m\)
B. Thợ thứ nhất: \(132m\); thợ thứ hai: \(126m\)
C. Thợ thứ nhất: \(117m\); thợ thứ hai: \(141m\)
D. Thợ thứ nhất: \(153m\); thợ thứ hai: \(105m\)
C. Thợ thứ nhất: \(117m\); thợ thứ hai: \(141m\)
- Tìm tổng số mét vải có nếu thợ thứ nhất dệt thêm \(36m\) vải và thợ thứ hai dệt bớt đi \(15m\) vải.
- Tìm số vải thợ thứ nhất dệt được nếu người đó dệt thêm \(36\) vải.
- Tìm số mét vải thực tế người thứ nhất dệt được.
- Tìm số mét vải thực tế người thứ hai dệt được.
Nếu thợ thứ nhất dệt thêm \(36m\) vải và thợ thứ hai dệt bớt đi \(15m\) vải thì hai người dệt được số mét vải là:
\(258 + 36 - 15 = 279\,\,(m)\)
Khi đó ta có sơ đồ:
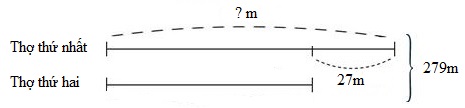
Nếu thợ thứ nhất dệt thêm \(36\) vải thì người đó dệt được số mét vải là:
\((279 + 27):2 = 153\,\,(m)\)
Thực tế người thứ nhất dệt được số mét vải là:
\(153 - 36 = 117\,\,(m)\)
Người thứ hai dệt được số mét vải là :
\(258 - 117 = 141\,\,(m)\)
Đáp số: Người thứ nhất: \(117m\);
Người thứ hai: \(141m\).