
Tí viết: “\(a \times b = b \times a\) ”. Bạn Tí viết đúng hay sai?
A. Đúng
B. Sai
A. Đúng
B. Sai
Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Nên : “\(a \times b = b \times a\) ”.
Vậy Tí viết đúng.

Sửu viết: “\(3925 \times 8 = 8 \times 3925\) ”. Sửu viết đúng hay sai?
A. Sai
B. Đúng
A. Sai
B. Đúng
Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Nên : “\(3925 \times 8 = 8 \times 3925\)”.
Vậy Sửu viết đúng.

Điền số thích hợp vào ô trống:
Cho \(1357 \times 4 = 5428\). Vậy $4 \times 1357 = $
Cho \(1357 \times 4 = 5428\). Vậy $4 \times 1357 = $
Áp dụng tính chất giao hoán của phép nhân: Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
\(a \times b = b \times a\)
Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Do đó: \(1357 \times 4 = 4 \times 1357\)
Mà \(1357 \times 4 = 5428\) nên \(4 \times 1357 = 5428\).
Vậy đáp án đúng điền vào ô trống là \(5428\).

Điền số thích hợp vào ô trống:
$6182 \times 7 =$
$ \times 6182$
$6182 \times 7 =$
$ \times 6182$
Áp dụng tính chất giao hoán của phép nhân: Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
\(a \times b = b \times a\)
Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Do đó ta có: \(6182 \times 7 = 7 \times 6182\)
Vậy đáp án đúng điền vào ô trống là \(7\).

Điền số thích hợp vào ô trống:
$972 \times$
$=$
$ \times 972 = 972$
$972 \times$
$=$
$ \times 972 = 972$
Áp dụng các tính chất:
- Tính chất giao hoán của phép nhân: Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
- Tính chất nhân với \(1\): số nào nhân với \(1\) cũng bằng chính số đó.
Số nào nhân với 1 cũng bằng chính nó nên \(972 \times 1 =972\)
Mà: \(972 \times 1 = 1 \times 972\)
Do đó ta có: \(972 \times 1 = 1 \times 972 = 972\).
Vậy số thích hợp điền vào ô trống từ trái sang phải là \(1;\,1\).

\(m \times n = n \times ...\).
Đáp án đúng điền vào chỗ chấm là:
A. \(0\)
B. \(1\)
C. \(m\)
D. \(n\)
C. \(m\)
Áp dụng tính chất giao hoán của phép nhân: Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Do đó ta có : \(m \times n = n \times m\)
Vậy đáp án đúng điền vào chỗ chấm là \(m\).

Cho biểu thức: $38756 \times 9 .$ Biểu thức nào sau đây có giá trị bằng biểu thức đã cho?
A. \(9 \times 37856\)
B. \(9 \times 38765\)
C. \(9 \times 37865\)
D. \(9 \times 38756\)
D. \(9 \times 38756\)
Áp dụng tính chất giao hoán của phép nhân: Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Do đó ta có: $38756 \times 9 = 9 \times 38756$
Vậy biểu thức có giá trị bằng với biểu thức $38756 \times 9$ là \(9 \times 38756\).

Điền số thích hợp vào ô trống:
$2020 \times 0 =$
$ \times 2020 =$
$2020 \times 0 =$
$ \times 2020 =$
- Áp dụng tính chất giao hoán của phép nhân: Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
- Mọi số nhân với \(0\) đều bằng \(0\) : \(a \times 0 = 0 \times a = 0\) .
Số nào nhân với \(0\) đều bằng \(0\) nên \(2020 \times 0 = 0\)
Mà: \(2020 \times 0 = 0 \times 2020\)
Do đó ta có: \(2020 \times 0 = 0 \times 2020 = 0\)
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(0\,\,;\,\,0\).

Cho: \(2389 \times 8\,\,...\,\,8 \times 2398\).
Dấu thích hợp điền vào chỗ chấm là:
A. \( < \)
B. \( > \)
C. \( = \)
A. \( < \)
Áp dụng tính chất giao hoán của phép nhân: Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Do đó ta có: \(2389 \times 8\,= \,8 \times 2389\)
Lại có \(2389 < 2398\) nên \(8 \times 2389 < 8 \times 2398\)
Vậy \(2389 \times 8\,< \,8 \times 2398\).

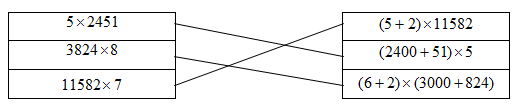
Ghép nối hai biểu thức có giá trị bằng nhau:
\(5 \times 2451\)
\(3824 \times 8\)
\(11582 \times 7\)
\((5 + 2) \times 11582\)
\((2400 + 51) \times 5\)
$(6+2) \times (3000+824)$
\(5 \times 2451\)
\((2400 + 51) \times 5\)
\(3824 \times 8\)
$(6+2) \times (3000+824)$
\(11582 \times 7\)
\((5 + 2) \times 11582\)
Áp dụng tính chất giao hoán của phép nhân: Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Ta có:
\(\begin{array}{l}(5 + 2) \times 11582 = 7 \times 11582 = 11582 \times 7\\(2400 + 51) \times 5 = 2451 \times 5 = 5 \times 2451\\(6 + 2) \times (3000 + 824) = 8 \times 3824 = 3824 \times 8\end{array}\)
Vậy ta có kết quả như sau:

Điền số thích hợp vào ô trống:
$175 \times 99 \times 8 = 8 \times 175 \times$
$175 \times 99 \times 8 = 8 \times 175 \times$
Áp dụng tính chất giao hoán của phép nhân: Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Do đó \(175 \times 99 \times 8 = 8 \times 175 \times 99\)
Vậy đáp án đúng điền vào ô trống là \(99\).

\(29548 \times 9 = 3 \times \,\,...\)
Đáp án đúng điền vào chỗ chấm là:
A. \(29548\)
B. \(29548 \times 9\)
C. \(29458\)
D. \(29548 \times 3\)
D. \(29548 \times 3\)
Áp dụng tính chất giao hoán của phép nhân: Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Do đó ta có: \(29548 \times 9 = 29548 \times 3 \times 3 = 3 \times 29548 \times 3\)
Vậy đáp án đúng điền vào chỗ chấm là \( 29548 \times 3\).

Điền số thích hợp vào ô trống:
Biết $81836 \times 7 \times 2 \times b = 7 \times 81836 \times 98 \times 2.$
Vậy $b =$
Biết $81836 \times 7 \times 2 \times b = 7 \times 81836 \times 98 \times 2.$
Vậy $b =$
Áp dụng tính chất giao hoán của phép nhân: Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Khi đổi chỗ các thừa số trong một tích thì tích đó không thay đổi.
Do đó ta có: \({\rm{7}} \times 81836 \times 98 \times 2 = 81836 \times 7 \times 2 \times 98\)
Theo đề bài: \(81836 \times 7 \times 2 \times b{\rm{ }}= {\rm{ 7}}\times 81836 \times 98 \times 2\)
Từ đó suy ra:
\(81836 \times 7 \times 2 \times b{\rm{ }}= {\rm{ }}81836 \times 7 \times 2 \times 98\)
Suy ra \(b = 98\).
Vậy đáp án đúng điền vào ô trống là \(98\).
